
Looking again at A$^\prime$ and A$^$ its midpoint lies at the origin (0,0), and the same is true for all other points. A vertical reflection reflects a graph vertically across the. The same calculations work for the other points: in each case, the $x$-coordinate does not change and the $y$-coordinate changes sign.īelow is a picture of the original points, their reflections over the $x$-axis and then the reflections of the new points over the $y$-axis: Another transformation that can be applied to a function is a reflection over the x- or y-axis. If we were to fold the plane along the $x$-axis, the points A and A$^\prime$ match up with one another. Reflecting over the $x$-axis does not change the $x$-coordinate but changes the sign of the $y$-coordinate. Similarly the coordinates of $B$ are $(-4,-4)$ while $C = (4,-2)$ and $D = (2,1)$.īelow is a picture of the reflection of each of the four points over the $x$-axis: Let, A(1, 5) be a point, and the line y x be the axis of reflection, the line y x is a line bisecting the angle between X-axis and Y-axis lying in the first. The coordinates of $A$ are $(-5,3)$ since $A$ is five units to the left of intersection of the axes and  3 units up. 3) reflection across the x-axis x y F G H 4) reflection across the y-axis x y N M L Find the coordinates of the vertices of each figure after the given transformation. Rewrite the transformation using reflection notation. In order to help identify patterns in how the coordinates of the points change, the teacher may suggest for students to make a table of the points and their images after reflecting first over the $x$-axis and then over the $y$-axis: Point y Graph the image of the figure using the transformation given. Thus the knowledge gained in this task will help students when they study transformations in the 8th grade and high school. Later students will learn that this combination of reflections represents a 180 degree rotation about the origin. This means that if we reflect over the $x$-axis and then the $y$-axis then both coordinates will change signs. Similarly when we reflect a point $(p,q)$ over the $y$-axis the $y$-coordinate stays the same but the $x$-coordinate changes signs so the image is $(-p,q)$.Â.If the negative sign belongs to the y, then the graph will flip about the x-axis. When we reflect a point $(p,q)$ over the $x$-axis, the $x$-coordinate remains the same and the $y$- coordinate changes signs so the image is $(p,-q)$. Remember Reflections: They appear like opposites.The teacher may wish to prompt students to identify patterns in parts (b) and (c): Based on the definition of reflection across the y-axis, the graph of y1(x) should look like the graph of f (x), reflected across the y-axis. For example, let’s say you had a point (1, 3) and wanted to reflect it over the x-axis.The goal of this task is to give students practice plotting points and their reflections. The above matrix A reflects a point (defined by column vector x) over the x-axis. In the Cartesian plane, a 2 x 2 matrix can describe a transformation on the plane. Matrix Operation for Reflection Over The X-Axis The last two easy transformations involve flipping functions upside down (flipping them around the x-axis), and mirroring them in the y-axis. The important part of the formula is the expression on the right hand side. Note: I’m using f(x) and g(x) here to name the functions, but you can name them anything you like (or use whatever names your instructor is using). Step 3: (Optional) Check your work by graphing both functions (your original function from the question and the one from Step 2) to make sure they are perfect reflections (I used ): Step 2: Remove the parentheses, carrying through the negative sign: Step 1: Place a negative sign in front of the right-hand side of the function:į(x) = x 2 – 3 becomes g(x) = – (x 2 – 3) When a function f(x) is reflected over the x-axis, it becomes a new function g(x) = – f (x).Įxample Question #2: What is f(x) = x 2 – 3 reflected over the x-axis?
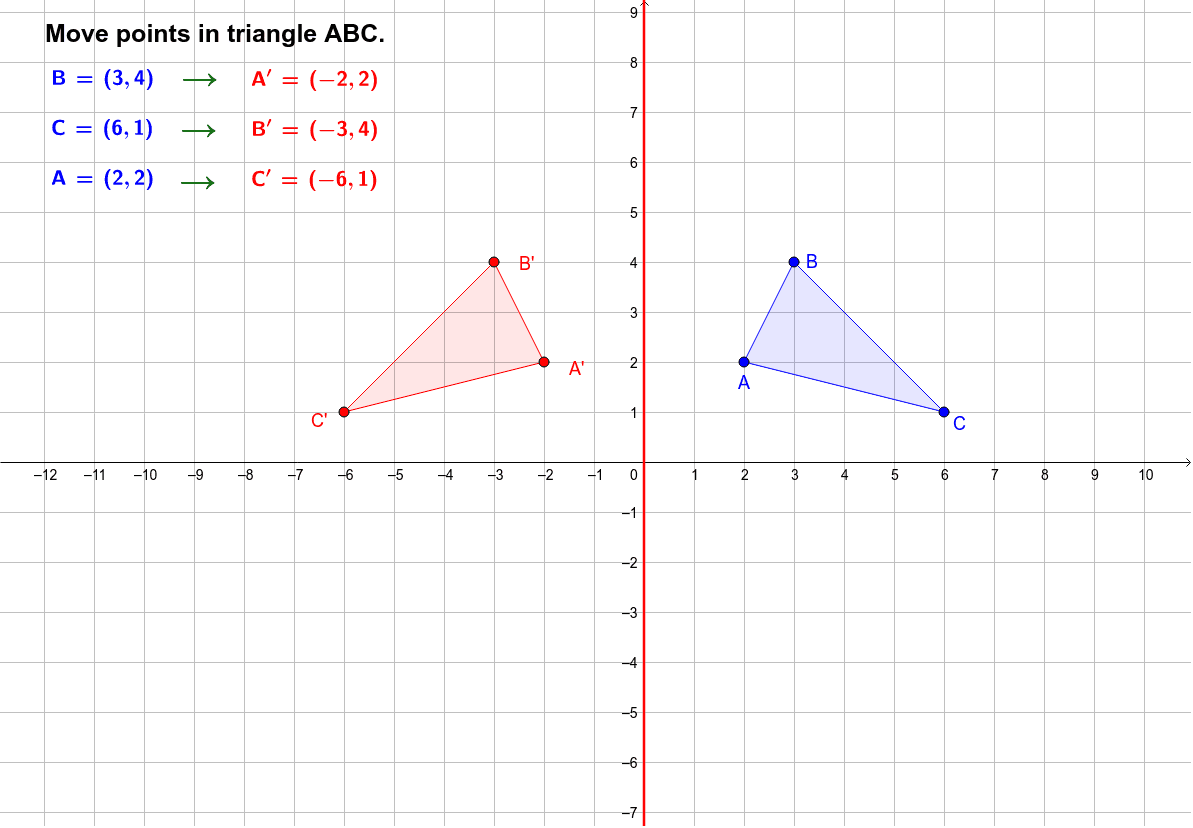
To reflect a function over the x-axis, multiply it by negative 1 (usually just written as “-“).

You can easily do this on : Just enter coordinates into the left hand column and check the “Label” box:
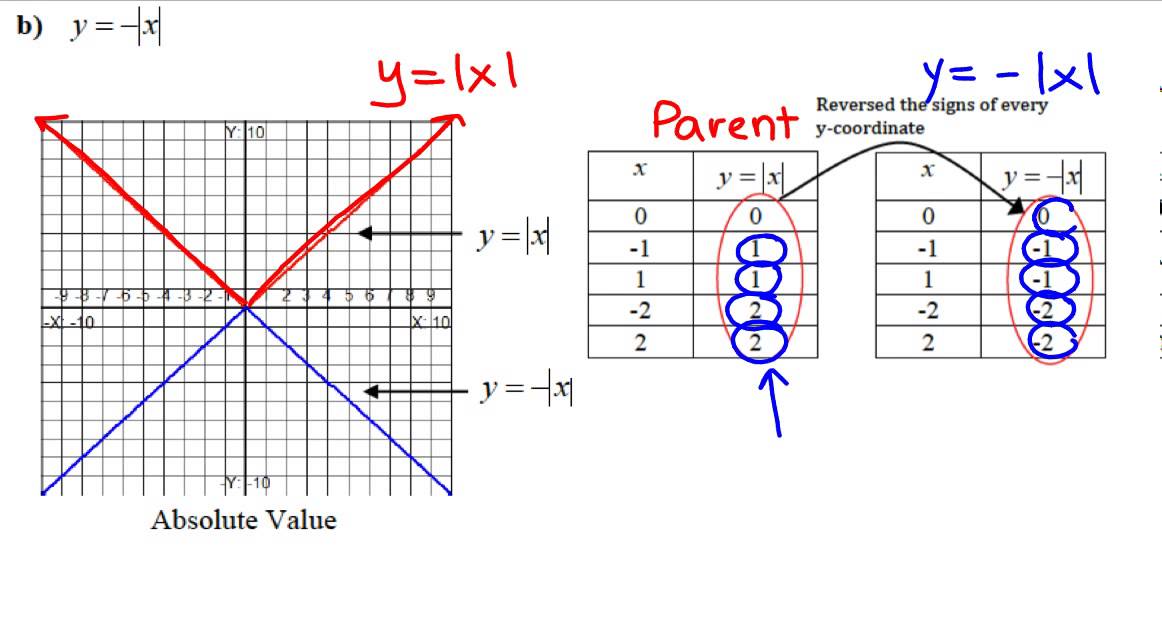
Step 2: (Optional) Plot both sets of coordinates (your original points and the ones from Step 2) to make sure you negated correctly.


 0 kommentar(er)
0 kommentar(er)
